Ground Up: State Machines
Welcome to a series of posts cleverly titled Ground Up, where I explain computing concepts from the ground up! We’ll explore how computers work starting with transistors and going from there. This post specifically covers finite state machines.
- [Part 1: Bits]({% post_url 2021-06-18-ground-up-bits %})
- [Part 2: Gates]({% post_url 2021-07-06-ground-up-gates %})
- [Part 3: Memory]({% post_url 2021-07-18-ground-up-memory %})
- Part 4: State Machines
State Machines
Finite state machines (FSMs) are a way to model solutions to problems. It describes the system as a machine that changes state in reaction to inputs to produce the appropriate outputs. There are two common types of finite state machines: Moore machines and Mealy machines. Moore machines define the outputs soley on the current state, while Mealy machines define the outputs on the current state and input values.
FSMs are used in a variety of useful products and services, such as combination locks, traffic lights, and elevators. Even part of a CPU uses a finite state machine for parsing and executing instructions, which is why we are learning about them.
Multiplexers
There is one important logic gate missing from our tool belt that will be very helpful in implementing a FSM: the multiplexer (MUX). I will leave the implementation details as an exercise to the reader and simply provide the truth table and schematic symbol.
| A | B | S0 | Z |
|---|---|---|---|
X | X | 0 | A |
X | X | 1 | B |
Essentially, the output Z is set to A if S0 is 0 and B if S0 is 1.
Designing a FSM
At this point in our journey, we have enough components to build a state machine circuit. We can store the current state in memory and use logic gates to determine the outputs. In this post, we will make a combination lock, where the user must input three numbers in the correct order to unlock the lock.
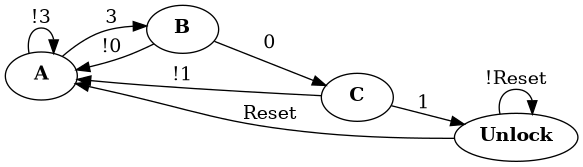 {: style=“width: fit-content; margin-left: auto; margin-right: auto;” }
{: style=“width: fit-content; margin-left: auto; margin-right: auto;” }
This FSM is a Moore machine with 4 states: A, B, C, and
Unlock. The text on the arrows are known as state transitions.
The diagram describes what happens when an input is received in each
state. Notice that the correct combination is 301 to reach the
Unlock state. There is also a Reset input that will immediately
reset the machine to the initial state.
Note: !x in the diagram indicates negation. It is a short-hand that
means any input besides x.
Because this is a Moore machine, we must define the output as a function of the state. We only have one output: Locked.
| Current State | Locked |
|---|---|
| A | 1 |
| B | 1 |
| C | 1 |
| Unlock | 0 |
| {: style=“width: 30%;” } |
Implementing a FSM
Now comes the technical nitty-gritty part. We need to build the FSM
with the building blocks we have. We have four states that we need to
remember, which can be encoded in two bits (00 01 10 11). We
will need a few button inputs as well: 0 1 2 3 and Reset. Let’s
make a truth table to help visualize the state transitions.
| S | B0 | B1 | B2 | B3 | R | S' | |
|---|---|---|---|---|---|---|---|
| A | 0 | 0 | 0 | 1 | 0 | B | |
| A | _ | _ | _ | _ | _ | A | |
| B | 1 | 0 | 0 | 0 | 0 | C | |
| B | _ | _ | _ | _ | _ | A | |
| C | 0 | 1 | 0 | 0 | 0 | Unlock | |
| C | _ | _ | _ | _ | _ | A | |
| Unlock | _ | _ | _ | _ | 0 | Unlock | |
| Unlock | _ | _ | _ | _ | 1 | A | |
| {: style=“width: 50%;” } |
Note: _ indicates “do not care” and was chosen instead of X
to reduce clutter.
The last puzzle piece is to think about the timing. How will we determine when a button is pressed or not to advance the state? I think the simplest solution is to OR all the input buttons together to determine when a button is pressed, so let’s go with that.
Instructions: toggle the inputs to see how the circuit reacts.
| S | Locked | |||||
|---|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 0 | A | 1 |
Conclusion
Using boolean logic and a bit of memory, we were able to create a simple finite state machine. We utilized a multiplexer to switch between the input combinations based on the current state in order to determine the next state. FSMs deterministically model solutions to problems in a manageable way, and are a very useful concept in both hardware and software domains.
As always if any parts were unclear, please feel free to contact me.