Finite State Machine
A finite state machine is a mathematical model of computation to define the solution to a problem. It describes the system as a machine that changes state in reaction to inputs to produce the appropriate outputs. State machines are usually defined with drawn diagrams or a table. Examples of each follow.
State Machine Model
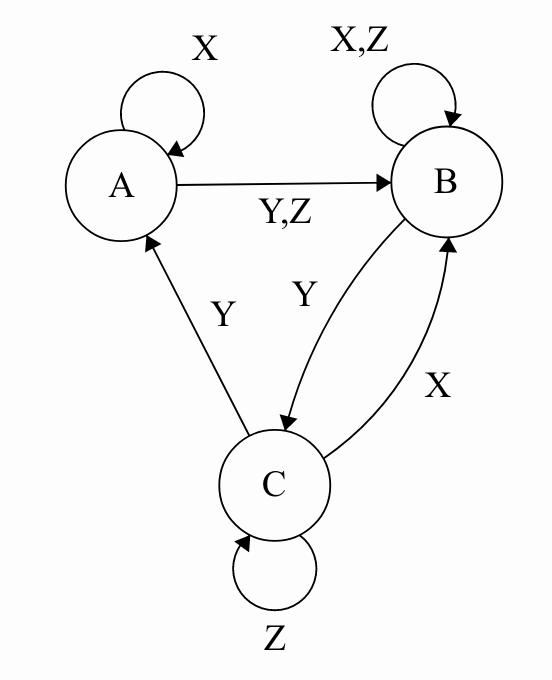
State Transition Table
| Input \ Current State | State A | State B | State C |
|---|---|---|---|
| Input X | State A | State B | State B |
| Input Y | State B | State C | State A |
| Input Z | State B | State B | State C |
Moore Machine
A Moore machine is a finite state machine whose output is determined solely by its current state. In the representation of a Moore machine, the output is written on the state. Generally, Moore machines require more states than Mealy machines.
Mealy Machine
A Mealy machine is a finite state machine whose output is determined by its current state and the input values. In representing a Mealy machine, the output is written on the transition arrows.